CIRCUITS ÉLECTRIQUES

CIRCUITS ÉLECTRIQUES

Un circuit ou réseau électrique est constitué par un ensemble de dispositifs qui assurent la production, le traitement et la conversion d’une énergie ou d’un signal électrique. Aussi, apparaît-il comme un constituant essentiel des montages de l’électrotechnique, de l’électronique et de l’automatique.

Les grandeurs fondamentales, généralement fonctions du temps t , qui caractérisent un élément de circuit, sont la différence de potentiel ou tension v(t ) existant à ses bornes et le courant i (t ) qui le parcourt; si l’une de ces grandeurs est imposée à un élément, elle constitue une excitation ou entrée e (t ), alors que la tension ou le courant résultant, relatif à un autre élément, constitue une réponse ou sortie s (t ) du réseau. L’étude du comportement d’un circuit, dont les éléments constituants sont connus, est un problème d’analyse qui consiste à calculer les différentes réponses s (t ) correspondant à des excitations e (t ) déterminées. D’autre part, on effectue la synthèse d’un réseau lorsqu’on détermine les éléments constituants qui permettent, à partir d’excitations e (t ) données, d’obtenir des réponses s (t ) fixées à l’avance.

Dans un circuit linéaire , les grandeurs e (t ) et s (t ) sont liées par des équations intégro-différentielles linéaires à coefficients constants . Les propriétés de l’opérateur linéaire conduisent alors au principe de superposition : si à des entrées e ¹(t ), e ²(t ), ..., e ^m (t ) correspondent respectivement des sorties s ¹(t ), s ²(t ), ..., s ^m (t ), à une entrée:

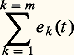correspond une sortie:

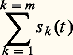À première vue, les réseaux linéaires paraissent des cas idéaux, de peu d’importance pratique, puisque, les caractéristiques de leurs constituants devant être indépendantes du temps, de la tension, du courant et de la température, cela semble éliminer la plupart des circuits et, notamment, tous ceux qui comportent des éléments semiconducteurs, ou doués d’hystérésis, ou encore saturables. En fait, dans la plupart des réseaux réels, il est possible de définir les zones de linéarité, d’où l’intérêt de l’étude correspondante.

On se limitera donc ici à l’étude des circuits linéaires, en insistant plus particulièrement sur le fonctionnement général des réseaux à constantes localisées et sur le comportement, en régime sinusoïdal, des multidipôles, qui constituent une catégorie très importante de circuits.

1. Circuits linéaires à constantes localisées

Éléments passifs et actifs

Les éléments passifs d’un réseau, qui ne peuvent que dissiper sous forme de chaleur ou emmagasiner de l’énergie, sont définis par une résistance R, une capacité C, une inductance propre L et une inductance mutuelle M; ces quatre constantes sont dites localisées lorsque le courant est le même, à un instant donné, dans chaque section de l’élément; l’approximation correspondante est valable, en particulier, lorsque la longueur de l’élément et la fréquence de la source alimentant le circuit sont suffisamment faibles. Les grandeurs R, C et L sont, par définition, positives et le courant et la tension à leurs bornes sont liés par la loi d’Ohm dont les différentes expressions avec les conventions de signe indiquées (v = v¹ 漣 v²), sont notées sur la figure 1.

La loi d’Ohm fournit également une expression des tensions aux bornes de deux inductances propres L¹ et L² couplées par une inductance mutuelle M (positive ou négative).

Les éléments actifs sont les sources d’excitation e (t ), sources de tension v(t ) ou de courant i (t ). Elles sont dites dépendantes ou indépendantes suivant que l’excitation qu’elles délivrent est fonction ou non de la tension ou du courant dans un autre élément. Les principaux types de sources sont les sources continues, qui produisent une excitation indépendante du temps t , et les sources alternatives, qui délivrent une excitation qui est généralement une fonction périodique (de période T) du temps t , donc telle que:

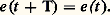D’après le théorème de Fourier, cette fonction est décomposable en une somme d’un terme constant et de fonctions sinusoïdales comportant un terme fondamental de pulsation 諸 = 2 神/T et des harmoniques de pulsations 2 諸, 3 諸, ..., n 諸; c’est-à-dire:

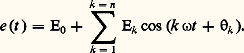L’application du principe de superposition, qui permet de définir la réponse du circuit comme la somme des réponses à chacun des termes de la série de Fourier, montre ainsi toute l’importance des excitations sinusoïdales.

Résolution des équations générales

Des dérivations successives permettent toujours de mettre la relation intégro-différentielle liant une excitation e (t ) et une réponse s (t ) sous la forme:

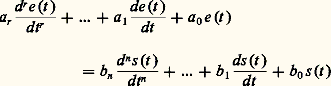Le régime correspondant est le plus commodément défini en utilisant le calcul symbolique , fondé sur la transformation de Laplace , qui fait correspondre à la fonction e (t ) ou s (t ) de la variable réelle t , la fonction E(p ) ou S(p ) de la variable complexe p = 靖 + j 諸. La fonction E(p ), image de e (t ), désignée par E(p ) = 硫e (t ), est définie par:

Inversement, e (t ) est l’original de E(p ), ce que l’on note: e (t ) = 硫^-1E(p ).

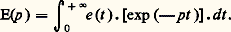Dans le cas où le réseau est au repos avant application de l’excitation, l’équation générale ci-dessus devient:

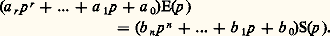On définit la transmittance ou fonction de transfert symbolique H(p ) par le rapport des deux polynômes en p , N(p ) et D(p ):

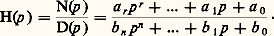La connaissance de H(p ) permet alors le calcul immédiat, du moins théoriquement, de s (t ); en effet, à e (t ) connu, correspond E(p ) = 硫e (t ); on en déduit S(p ) = H(p )E(p ) et enfin s (t ) = 硫^-1S(p ), original de S(p ).

On montre que la réponse s (t ) comporte deux sortes de termes: ceux qui dépendent de l’excitation appliquée et définissent le régime forcé ou permanent et ceux qui dépendent de la morphologie et de l’état initial du circuit et définissent le régime libre . Ce régime libre, dans lequel interviennent des termes de la forme exp (p ^Dt ), où les p ^D sont les racines de l’équation D(p ) = 0, s’évanouit plus ou moins rapidement dans un réseau stable, car la partie réelle des p ^D est négative. Le comportement du réseau est alors défini par le seul régime permanent.

Dans le cas d’une excitation continue e (t ) = E = constante, le calcul du régime permanent, qui fait seulement intervenir les résistances du circuit, ne rencontre aucune difficulté.

Dans le cas d’une excitation sinusoïdale de valeur efficace E, donc d’amplitude E^m = E 連2, de fréquence f = 諸/2 神 et de phase , soit:

la réponse en régime permanent est une fonction sinusoïdale de même pulsation , donc de la forme: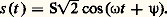

Cette réponse est aisément calculée d’après les expressions symboliques précédentes, dans lesquelles la pulsation complexe p est remplacée par la pulsation imaginaire j 諸; les grandeurs symboliques E(p ), S(p ) et H(p ) deviennent des grandeurs complexes, notées E^m = E 連2, S^m = S 連2 et H, avec E = E exp (j ) et S = S exp (j 祥). La transmittance complexe , H = H exp (j 益), définit alors entièrement, par son module H et son argument 益, la réponse instantanée s (t ), puisque S = H . E et 祥 = + 益. Dans le cas où e (t ) et s (t ) sont de nature différente (tension et courant), H est appelée immitance complexe ; c’est une impédance lorsque l’excitation est un courant et la réponse une tension, une admittance dans le cas contraire.

Parmi les moyens d’étude des transmittances symboliques H(p ), les plus utilisés sont la méthode des schémas fonctionnels ou schémas blocs et la méthode des graphes de fluence .

L’étude des variations de la transmittance complexe H d’un réseau en fonction de la pulsation 諸 constitue l’analyse harmonique du système; elle permet, d’une part, de déterminer le comportement d’un réseau soumis à une excitation périodique non sinusoïdale décomposée en série de Fourier, d’autre part, de caractériser un système donné à partir d’essais à différentes fréquences. On peut citer, parmi les représentations graphiques utilisées, le diagramme de Bode et le diagramme de Nyquist .

Définitions topologiques et applications

La plupart des réseaux électriques sont maillés , c’est-à-dire que leurs éléments sont assemblés de façon à former un certain nombre de circuits fermés (fig. 2).

On appelle: nœud (n ), un point de jonction de plusieurs conducteurs; branche (b ), une portion de circuit comprise entre deux nœuds; maille , un ensemble de branches formant un parcours fermé; graphe , la représentation schématique du réseau obtenue en remplaçant les branches par des traits et les nœuds par des points; arbre , tout ensemble de branches, simplement connexe, joignant tous les nœuds et ne formant aucune maille; branche complémentaire d’un arbre , toute branche du réseau n’appartenant pas à l’arbre considéré. On peut évidemment définir plusieurs arbres dans un graphe déterminé, mais le nombre de leurs branches est toujours t = n 漣 1, alors que le nombre de branches complémentaires est c = b 漣 t = b 漣 n + 1.

Des méthodes matricielles permettent de calculer les tensions et les courants dans les b branches du réseau à partir des sources d’excitation et de la matrice carrée d’ordre b dont les termes sont les impédances propres et mutuelles des différentes branches; dans la méthode des nœuds, interviennent les tensions indépendantes qui sont au nombre de t ; dans la méthode des mailles, interviennent les courants indépendants , au nombre de c . En dehors de leur intérêt systématique, ces méthodes fournissent une démonstration simple du théorème de réciprocité (Maxwell), qui s’énonce ainsi: Si, dans un réseau passif , l’insertion d’une tension v dans une branche k provoque la circulation d’un courant i dans une branche l , l’insertion de la tension v dans la branche l provoquera la circulation du même courant i dans la branche k .

2. Étude des multidipôles en régime sinusoïdal permanent

Parmi les réseaux les plus fréquemment utilisés, il faut citer les multidipôles ou multiportes , dont la liaison avec le milieu extérieur s’effectue par l’intermédiaire d’un nombre pair 2 m de bornes, repérées par couples, tels que le courant entrant par une borne a ^k du couple sorte obligatoirement par l’autre borne a ^k .

Dipôles passifs et actifs

Le dipôle ou monoporte , défini par m = 1, est le plus simple des multidipôles.

Dans un dipôle passif , qui ne comporte aucune source, à l’application d’une tension v(t ) = V 連2 cos ( 諸 t + ) correspond un courant i (t ) = I 連2 cos ( 諸 t + 漣 﨏). La loi d’Ohm V = Z I montre que le courant est entièrement déterminé par la connaissance de l’impédance complexe du dipôle Z = Z exp (j 﨏) = R + j X. La partie réelle R de Z, ou résistance , et la partie imaginaire X, ou réactance , sont liées par la relation X = R tg 﨏 (fig. 3).

Le diagramme de Fresnel traduit vectoriellement à partir d’un axe origine Ox , la représentation complexe précédente (fig. 4).

Dans un circuit purement résistant, le courant est en phase avec la tension ( 﨏 = 0); il est en retard sur la tension ( 﨏 礪 0) dans un circuit à prépondérance inductive, et en avance ( 﨏 麗 0) dans un circuit à prépondérance capacitive. Les composantes du vecteur と en phase et en quadrature avec ふ définissent respectivement le courant actif I^a = I cos 﨏 et le courant réactif I^r = I sin 﨏.

La loi d’Ohm peut s’écrire également, en définissant l’admittance complexe Y = 1/Z = 1/Z exp (face=F0019 漣 j 﨏) = G + j B, sous la forme I = Y V. La partie réelle G de Y est la conductance et la partie imaginaire B la susceptance du dipôle.

Le calcul de l’impédance Z ou de l’admittance Y d’un dipôle peut souvent s’effectuer en groupant en série ou en parallèle certains éléments constituants. Comme le montre l’application de la loi des mailles de Kirchhoff , l’impédance Z d’un ensemble de n éléments groupés en série est égale à la somme des impédances complexes de chaque élément. De même, l’admittance Y d’un ensemble de n éléments groupés en parallèle est égale, d’après la loi des nœuds de Kirchhoff , à la somme des admittances complexes de chaque élément (fig. 5).

La puissance active , dépensée dans un dipôle passif, valeur moyenne du produit vi , s’écrit:

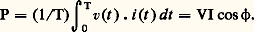Elle s’exprime en watts (W) si V est en volts (V) et I en ampères (A); elle fait intervenir le facteur de puissance cos 﨏 du circuit. Comme il est impossible de définir la puissance active d’un générateur, puisqu’elle dépend de 﨏, donc du récepteur alimenté, on introduit la puissance apparente S = VI, qui s’exprime en volts-ampères (VA). La puissance active s’écrit également, en fonction du courant actif (voir la représentation de Fresnel, fig. 4): P = VI^a . Par analogie, on appelle puissance réactive , la quantité Q = VI^r = VI sin 﨏, qui s’exprime en volts-ampères réactifs (vars). On peut remarquer que P et Q apparaissent respectivement comme la partie réelle et la partie imaginaire de la puissance complexe :

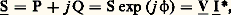où I désigne le nombre complexe conjugué de I.

Un dipôle actif contient des sources d’excitation, c’est-à-dire des sources de tension E^s d’impédance interne Z^s ou des sources de courants I^s d’admittance interne Y^s (fig. 6).

La tension délivrée par la source de tension est V = E^s 漣 Z^s I et le courant fourni par la source de courant est I = I^s 漣 Y^s V. On en déduit qu’une source d’excitation, qui débite un courant i sous une tension v, peut être considérée soit comme une source de tension, soit comme une source de courant à condition que leurs caractéristiques soient liées par:

Pour calculer le courant débité par un dipôle actif dans une impédance Z (ou une admittance Y = 1/Z), on a très souvent intérêt à employer le schéma de Thévenin , dans lequel on remplace le dipôle par une source de tension V⁰ («tension à vide» existant entre a et a avant introduction de Z) d’impédance interne Zⁱ (impédance du dipôle rendu passif, c’est-à-dire dont les sources sont supprimées), ou le schéma de Norton , qui fait intervenir une source de courant («courant de court-circuit» entre a et a directement reliés) d’admittance interne Yⁱ (fig. 7).

Quadripôles passifs

Un quadripôle passif ou biporte Q est un multidipôle à deux paires de bornes qui intervient généralement comme un organe de liaison entre un réseau 倫¹, relié aux bornes d’entrée a ¹, a ¹, et un réseau 倫² relié aux bornes de sortie a ², a ² (fig. 8).

Pour établir les équations du système, on suppose d’abord que le quadripôle est alimenté par V¹ entre a ¹ et a ¹ et que les bornes a ² et a ² sont mises en court-circuit; le réseau est alors un dipôle, et il existe entre le courant dans une branche quelconque et la tension V¹ une relation linéaire faisant intervenir des admittances; on en déduit le courant à l’entrée, de la forme I¹¹ = Y¹¹V¹ et le courant à la sortie I²¹ = Y²¹V¹. L’alimentation par V² entre a ² et a ¹ conduit, de la même façon, à l’expression des courants à l’entrée I¹² = Y¹²V² et à la sortie I²² = Y²²V². L’application du principe de superposition fournit alors l’équation générale, écrite sous forme matricielle: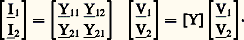

La matrice admittance [Y] est antisymétrique, le théorème de réciprocité imposant, compte tenu des sens positifs choisis pour I¹ et I², la relation Y²¹ = 漣 Y¹².

L’équation ci-dessus peut s’écrire, en considérant la matrice impédance [Z], inverse de [Y], donc également antisymétrique:

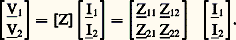On définit couramment deux autres types de matrices: la matrice de transfert [T], liant le régime à l’entrée au régime à la sortie:

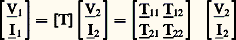et la matrice hybride [H], très utile pour l’étude des transistors:

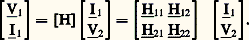Les coefficients de ces différentes matrices se calculent aisément en fonction les uns des autres; en particulier le caractère d’anti-symétrie des matrices [Z] et [Y] impose la valeur 1 au déterminant de la matrice [T], soit T¹¹T²² 漣 T¹²T²¹ = 1.

Un quadripôle est symétrique lorsque l’inversion des bornes d’entrée et de sortie ne modifie pas les régimes des réseaux extérieurs 倫¹ et 倫². Entre les termes des matrices caractéristiques existe alors une relation supplémentaire: pour la matrice [T], on a par exemple T¹¹ = T²².

Les quadripôles peuvent être groupés entre eux de différentes façons; les dispositions les plus courantes sont les couplages en série, en parallèle et en cascade (fig. 9). Dans ce dernier cas, l’ensemble est équivalent à un quadripôle de matrice de transfert:

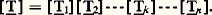Les montages en cascade de quadripôles trouvent une application intéressante dans les filtres électriques qui arrêtent ou laissent passer les courants, suivant les bandes de fréquences auxquelles ils appartiennent.

Systèmes polyphasés

Un système polyphasé est un multidipôle actif dans lequel les circuits reliés à chaque paire de bornes sont indépendants; chacun de ces circuits constitue une phase du système. La plupart des générateurs et des moteurs de forte puissance comportent trois phases; les systèmes triphasés correspondants sont, de plus, équilibrés , c’est-à-dire que l’impédance de chaque phase est la même et que les tensions sinusoïdales aux bornes, de même valeur efficace V, sont régulièrement déphasées de 2 神/3:

Le signe 漣 définit un système direct , dont la représentation complexe est, en introduisant l’opérateur a :

Le signe + définit un système inverse , représenté par: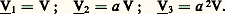

Si chaque phase est chargée sur la même impédance Z = Z exp (j 﨏), les courants j ¹, j ², j ³, de même valeur efficace J = V/Z sont déphasés du même angle 﨏 par rapport aux tensions correspondantes (fig. 10 a). Ces systèmes triphasés permettent, en particulier, par un groupement judicieux des phases, de ramener de six à trois ou quatre le nombre de fils nécessaires à la transmission d’énergie d’un générateur à un récepteur.

Dans le montage en étoile , les bornes homologues a ^j sont réunies en un point commun N, appelé point neutre (fig. 10 b). La valeur efficace du courant I dans un fil de ligne est égale à celle du courant J dans une phase; mais la valeur U de la tension entre deux fils de ligne est différente de V; on a par exemple U size=1^漣12 = V¹ 漣 V², soit, d’après le diagramme vectoriel, U = V 連3. Les distributions d’énergie électrique à basse tension sont réalisées à partir d’un générateur monté en étoile et possédant de plus un fil neutre NN ; les installations d’éclairage L¹, L², L³ sont réparties entre chaque fil de ligne et le fil neutre; en France, les tensions de distribution sont normalisées aux valeurs V = 220 volts et U = 380 volts.

Le montage triangle , réalisable uniquement sur les systèmes équilibrés en tensions (v¹ + v² + v³ = 0), est obtenu en reliant les phases bout à bout par leurs bornes non homologues; la valeur de la tension U entre deux fils de ligne est égale à V, mais la valeur du courant de ligne I est différente de celle du courant de phase J; on a, par exemple: I 漣³¹ = J³ 漣 J¹, soit, d’après le diagramme vectoriel: I = J 連3 (fig. 10 c).

On peut toujours déterminer les éléments caractéristiques du montage étoile correspondant à un montage triangle donné et l’étude du système est réalisée le plus commodément en introduisant un schéma monophasé équivalent , faisant intervenir les impédances cycliques , ou impédances équivalentes par phase. La connaissance du régime pour une phase (v^k et j ^k dans la phase k , avec k = 1, 2, ou 3) suffit pour caractériser le système tout entier, puisque la tension et le courant d’une autre phase ont, par rapport à v^k et j ^k , la même valeur efficace (V et J) et des phases décalées de 梁 2 神/3.

Dans un système triphasé déséquilibré , les tensions et les courants de chaque phase ont toujours la même pulsation 諸, mais leurs amplitudes et leurs phases sont quelconques; on a, par exemple, pour les tensions:

qui correspondent aux valeurs complexes V¹ = V¹ exp(j ¹), V² = V² exp(j ²) et V³ = V³ exp(j ³).

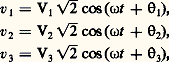L’étude de ces systèmes est généralement compliquée, car il est souvent impossible de définir leurs différentes impédances. La meilleure solution consiste à introduire les composantes symétriques des courants et des tensions, par exemple V^o , Vⁱ , V^d données par la relation matricielle:

avec a = exp(j (2 神/3)).

On obtient en effet, par inversion de la matrice carrée précédente: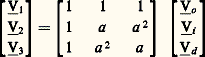

ce qui montre que le système des tensions est équivalent à la superposition de trois systèmes:

– un système direct V^d , a ²V^d , a V^d ,

– un système inverse Vⁱ , a Vⁱ , a ²Vⁱ ,

– un système homopolaire V^o , V^o , V^o , constitué de trois tensions identiques.

On peut alors définir les impédances relatives à chaque système et le régime total est obtenu en appliquant le principe de superposition.

3. Circuits linéaires à constantes réparties

Constantes linéiques

Les circuits précédents sont tous à constantes localisées, c’est-à-dire qu’en régime sinusoïdal permanent les impédances et admittances des divers éléments passifs sont situées tout entières entre deux points bien déterminés. L’approximation correspondante n’est valable qu’à condition que la longueur de l’élément soit très inférieure à la longueur d’onde de propagation des ondes électromagnétiques = c ; la vitesse c de ces ondes étant égale à 3 練 10⁵ km par seconde dans le vide (et pratiquement dans l’air), on en déduit qu’à la fréquence f = 50 Hz ( = 6 000 km), l’approximation est valable pour tous les dispositifs, sauf pour les longues lignes de transport d’énergie, alors qu’en très haute fréquence (par exemple: f = 10¹⁰ Hz, = 3 cm), il est impossible de localiser les constantes de tous les dispositifs, même les plus courts, car le courant n’est plus le même dans leurs différentes sections.

C’est ainsi que tout circuit bifilaire homogène, de longueur D, doit être décomposé en m = D/ x tronçons, de longueur x faible devant, localisables. On peut donc, par passage à la limite, affecter chaque élément dx d’une impédance d Z^s en série et d’une admittance d Y^d en dérivation; en explicitant les parties réelles et imaginaires de ces immittances, soit:

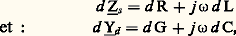on est amené à définir les constantes linéiques du circuit: résistance linéique r = d R/dx , inductance linéique l = d L/dx , conductance linéique g = d G/dx et capacité linéique c = d C/dx . À partir de ces grandeurs, calculables suivant la constitution du circuit, on exprime l’impédance linéique face="EU Domacr" 奈 ^s = r + jl 諸 et l’admittance linéique : face="EU Domacr" 喇 ^d = g + jc 諸; d’où: d Z^s = face="EU Domacr" 奈 ^s dx et d Y^d = face="EU Domacr" 喇 ^d dx (fig. 11).

Régime sinusoïdal permanent et régime transitoire d’une ligne bifilaire

Régime permanent

Dans une ligne bifilaire, alimentée en a ¹a ¹ sous une tension sinusoïdale v¹ de pulsation 諸 et fermée en a ² a ² sur une impédance de charge Z², la tension et le courant en tout point d’abscisse x (0 麗 x 麗 D) sont des fonctions sinusoïdales de même pulsation 諸, définies par leurs valeurs complexes.

D’autre part, la ligne est assimilable à un quadripôle, équivalent au montage en cascade de m quadripôles élémentaires identiques Q¹, ..., Q^j , ..., Q^m ; on en déduit l’expression de la matrice de transfert en fonction de l’impédance caractéristique face="EU Domacr" 奈 ^c = 連 face="EU Domacr" 奈 ^s / face="EU Domacr" 喇 ^d et de la constante de propagation face="EU Domacr" 滑 = 連 face="EU Domacr" 奈 ^s . face="EU Domacr" 喇 ^d ; l’équation générale de la ligne est alors:

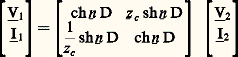Plus généralement, le régime (V^x , I^x ) au point courant, d’abscisse x , qui se déduit de la relation précédente en faisant D = x , peut également s’écrire, en désignant par face="EU Domacr" 車 ⁱ et face="EU Domacr" 車 ^r deux quantités complexes, dépendant du régime en a ²a ²:

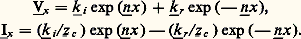Ces deux équations permettent l’étude de la ligne par la méthode des ondes mobiles . En effet, en désignant par a et b les parties réelle et imaginaire de n size=1^漣 et par k ⁱ , k ^r et 塚ⁱ , 塚^r les modules et arguments de k size=1^{漣 i} et k size=1^{漣 r} , la première relation s’écrit, en valeurs instantanées: v^x = vⁱ + v^r , avec:

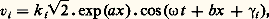qui représente une onde incidente de tension qui se propage dans le sens des x négatifs et s’amortit avec la constante d’atténuation a dans le sens de la propagation, et:

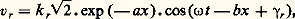qui représente une onde réfléchie , qui se propage en sens inverse, et s’amortit de même.

Des considérations analogues sont valables pour le courant que l’on écrit également sous la forme: i ^x = i ⁱ + i ^r .

Régime transitoire

Comme pour les circuits à constantes localisées, le régime transitoire des circuits à constantes réparties est étudié en général par l’intermédiaire de la transformation de Laplace ; une difficulté supplémentaire provient du fait que les tensions et les courants en un point sont fonction non seulement du temps, mais encore de l’abscisse du point considéré.

Encyclopédie Universelle. 2012.